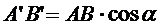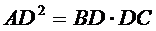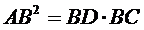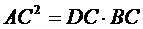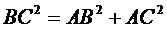Relaţii metrice în triunghiul dreptunghic programa matematica definitivat 2019

RELATII METRICE IN TRIUNGHIUL DREPTUNGHIC

1.1. Proiectii ortogonale pe o dreapta

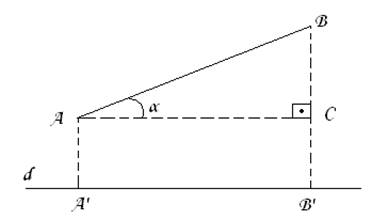
·Proiectia ortogonala a unui punct pe o dreapta este piciorul perpendicularei duse din acel punct pe dreapta.

·Proiectia ortogonala a unui segment pe o dreapta este un segment sau un punct.

Lungimea proiectiei :

1.2. Teorema inaltimii

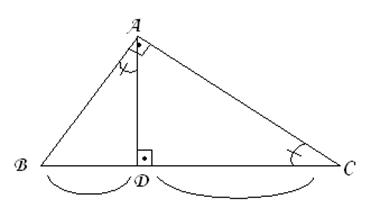
    Lungimea inaltimii unui triunghi dreptunghic, corespunzatoare ipotenuzei, este medie proportionala a proiectiilor catetelor pe ipotenuza.

1.3. Teorema catetei

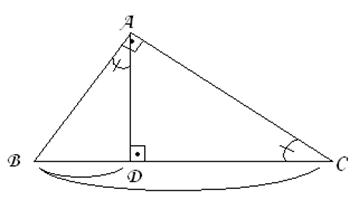
    Lungimea oricarei catete a unui triunghi dreptunghic este medie proportionala intre lungimea ipotenuzei si a proiectiei catetei respective pe ipotenuza.

1.4. Teorema lui Pitagora

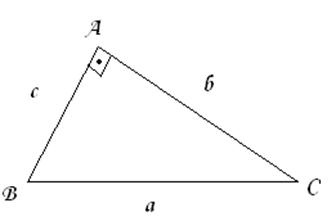
    Intr-un triunghi dreptunghic patratul lungimii ipotenuzei este egal cu suma patratelor lungimilor catetelor.

1.5. Teorema cosinusului

    Intr-un triunghi ABC au loc egalitatile :

a² = b² + c² - 2bc cos A

b² = c² + a² - 2ac cos B

c² = a² + b² - 2ab cos C

         OBSERVATIE

    In cazul in care m(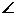A) = 90°, produsul scalar  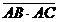= 0 si se obtine relatia

b² + c² = a², deci teorema lui Pitagora pentru triunghiul dreptunghic. De aceea, teorema cosinusului reprezinta teorema lui Pitagoma generalizata sub forma trigonometrica.

    Folosind teorema cosinusului se pot determina masurile unghiurilor unui triunghi in functie de laturile acestuia.

    Astfel, , , .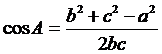

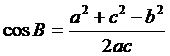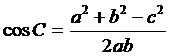1.6. Teorema sinusurilor

    Intr-un triunghi oarecare ABC au loc egalitatile .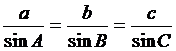

    Demosntratie

    Daca triunghiul ABC este dreptunghic (de exemplu in A), relatia se verifica imediat, deoarece sin A = 1, , .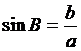

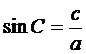    Sa consideram ABC triunghi care nu este dreptunghic si fie 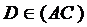. Perpendiculara in D pe AC intersecteaza BC in E.

    Asadar, a sin C = c sin A sau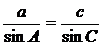 

_{sursa:.rasfoiesc.com}